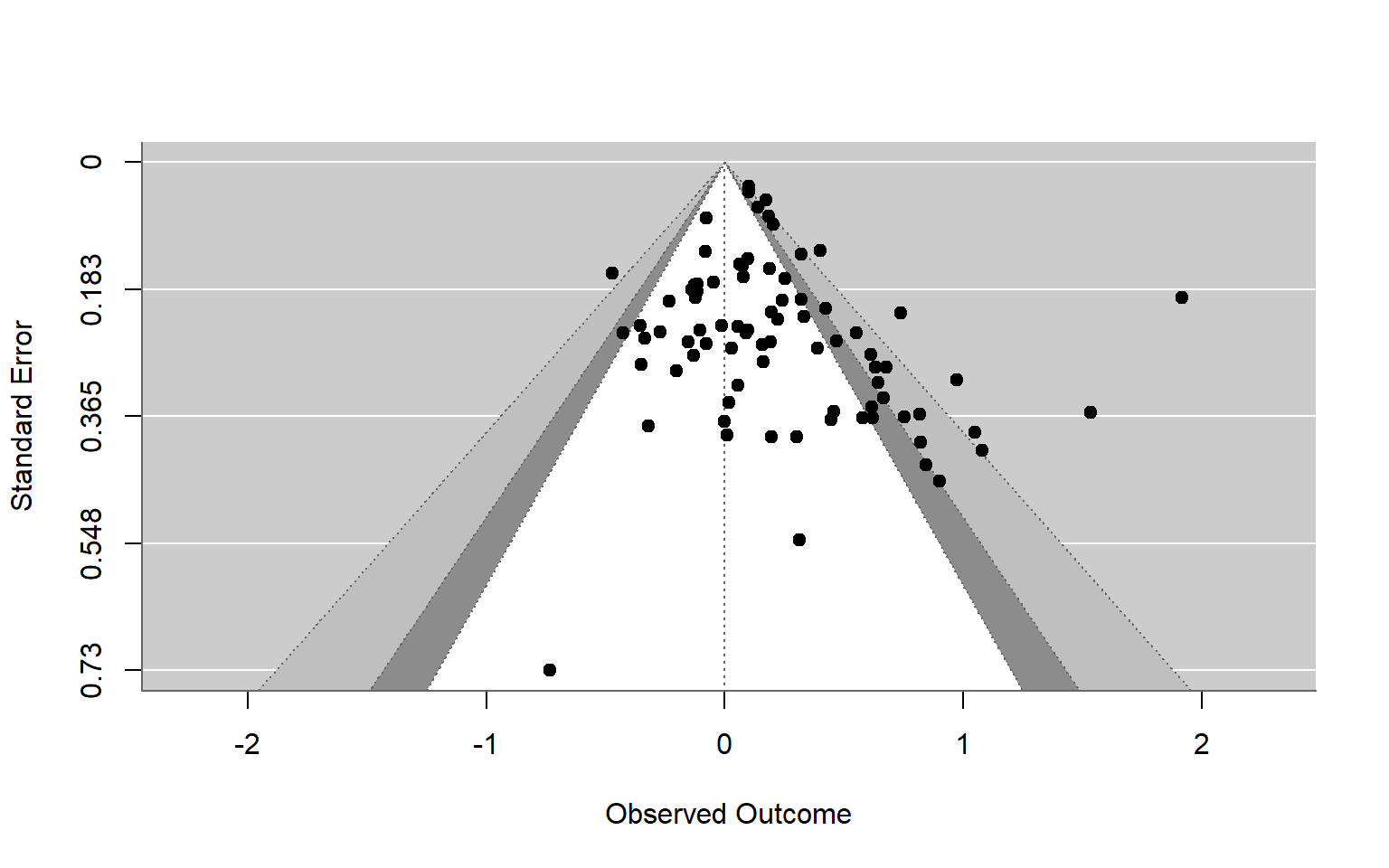
| Banas, 2014 |
Paper |
0.06 |
0.10 |
Banas, 2014 - Exp 1 |
Banas, K. (2014, July 7). Replication of Elliot et al. (2010) for CREP at the University of Edinburgh. Retrieved from osf.io/cvdpw |
2014.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
Scotland |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
20.43 |
20.95 |
LCh(50.0, 59.6, 31.3) |
LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
20 |
6.05 |
1.59 |
19 |
5.96 |
1.49 |
NA |
NA |
0.62 |
NA |
39 |
NA |
| Berthold, 2013 |
Screen |
0.55 |
0.06 |
Berthold, 2013 - Exp 1 - In Group |
Berthold, A. (2013). Unpublished data |
2013.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
4 |
1-7 |
1 |
7 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
25.00 |
25.00 |
No Data |
No Data |
No |
No |
Yes |
36 |
2.31 |
1.29 |
33 |
1.73 |
0.65 |
NA |
NA |
0.12 |
NA |
69 |
NA |
| Bigelow et al., 2013 |
Screen |
0.31 |
0.30 |
Bigelow et al., 2013 - Exp 1 |
Bigelow, M.G., Taylor, G. & Underwood, M. (2013). Context-moderated effect of color on physiological and self-report measures of emotional response. UNC Asheville Journal, Undergraduate Research Program, Asheville, NC |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Background |
Head Shot |
Same between conditions |
Single item |
1 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
NA |
NA |
NA |
NA |
NA |
NA |
Lab(37.43/59.24/47.63) |
Lab(36.68/34.86/87.99) |
No |
No |
Yes |
6 |
5.22 |
1.77 |
8 |
4.56 |
2.09 |
NA |
NA |
0.44 |
NA |
14 |
NA |
| Bigelow et al., 2013 |
Screen |
-0.73 |
0.53 |
Bigelow et al., 2013 - Exp 1 |
Bigelow, M.G., Taylor, G. & Underwood, M. (2013). Context-moderated effect of color on physiological and self-report measures of emotional response. UNC Asheville Journal, Undergraduate Research Program, Asheville, NC |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Background |
Head Shot |
Same between conditions |
Single item |
1 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
NA |
NA |
NA |
NA |
NA |
NA |
Lab(37.43/59.24/47.63) |
Lab(36.68/34.86/87.99) |
No |
No |
Yes |
4 |
4.65 |
2.05 |
4 |
6.28 |
1.81 |
NA |
NA |
0.66 |
NA |
8 |
NA |
| Blech, 2014 |
Screen |
0.08 |
0.03 |
Blech, 2014 - Exp 1 |
Blech, C. (2014, August 4). Replication of Elliot et al. (2010). Red, rank, and romance in women viewing men. Retrieved from osf.io/tx2u5 |
2014.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Head Shot |
Same between conditions |
Perceived attractiveness, German translation |
4 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
NA |
NA |
No Data |
No Data |
No |
No |
No |
71 |
5.36 |
1.43 |
78 |
5.25 |
1.48 |
NA |
NA |
0.53 |
Not part of CREP because Used white as control condition, dropped yellow as not an original control color, age not included because separated into categories (<25, 26-40, >=41) |
149 |
NA |
| Blech, 2015 |
Screen |
-0.35 |
0.05 |
Blech, 2015 - Class Exp |
Blech, C. (2015). Unpublished data from a class experiment |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
4 |
1-9 |
1 |
9 |
Germany |
Europe |
Adults |
NA |
Between Subjects |
White |
White |
White |
Matched |
31.40 |
31.40 |
NA |
NA |
No |
No |
No |
37 |
3.95 |
1.29 |
37 |
4.45 |
1.50 |
NA |
NA |
0.43 |
NA |
74 |
NA |
| Boelk & Madden, 2014 |
Paper |
-0.27 |
0.06 |
Boelk & Madden, 2014 - Exp 1 |
Boelk, K., & Madden, W. (2014, August 5). Fork of Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Retrieved from osf.io/zf7c9 |
2014.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
19.06 |
19.35 |
LCh(50.0, 59.6, 31.3) |
LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
34 |
6.03 |
1.24 |
34 |
6.40 |
1.49 |
NA |
NA |
0.68 |
NA |
68 |
NA |
| Buechner et al., 2015 |
Paper |
0.68 |
0.09 |
Buechner et al., 2015 - Exp 1 - Prideful Pose |
Buechner, V. L., Maier, M. A., Lichtenfeld, S., & Elliot, A. J. (2015). Emotion Expression and Color: Their Joint Influence on Perceived Attractiveness and Social Position. Current Psychology, 34(2), 422-433. http://doi.org/10.1007/s12144-014-9266-x |
2015.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Dot |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
High School |
Between Subjects |
White |
White |
White |
Matched |
16.88 |
16.88 |
LCh(50.9, 59.7, 25.7) |
LCh(49.2, 60.2, 278.2) |
Yes |
Yes |
Yes |
21 |
4.30 |
1.65 |
29 |
3.21 |
1.53 |
NA |
NA |
0.28 |
NA |
50 |
NA |
| Costello et al., 2017 |
Paper |
-0.12 |
0.03 |
Costello et al., 2017 - Exp 1 |
Costello J., Groeneboom L. & Pollet T. (2017). Romantic red: Do red products enhance the attractiveness of the consumer? Unpublished masters degree manuscript, University of Leiden |
2017.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Item |
Bust |
Same between conditions |
Single item perceived attractiveness |
1 |
1-5 |
1 |
5 |
Netherlands |
Europe |
Students |
Undergrad |
Between Subjects |
White |
White |
Asian |
Mis-match |
22.60 |
NA |
NA |
NA |
No |
No |
Yes |
65 |
2.25 |
1.04 |
64 |
2.38 |
0.95 |
NA |
NA |
0.34 |
NA |
129 |
NA |
| Costello et al., 2017 |
Paper |
0.08 |
0.02 |
Costello et al., 2017 - Exp 2 |
Costello J., Groeneboom L. & Pollet T. (2017). Romantic red: Do red products enhance the attractiveness of the consumer? Unpublished masters degree manuscript, University of Leiden |
2017.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Blue/Green |
Item |
Head Shot |
Same between conditions |
Single item perceived attractiveness |
1 |
1-5 |
1 |
5 |
Netherlands |
Europe |
Students |
Undergrad |
Between Subjects |
White |
White |
White |
Matched |
21.32 |
21.06 |
No Data |
No Data |
No |
No |
Yes |
67 |
2.60 |
1.37 |
140 |
2.49 |
1.38 |
NA |
NA |
0.37 |
Same filters applied as in Exp 1 (excluded homosexual and preferred not to answer). Control combines blue and green |
207 |
NA |
| Elliot & Maier, 2013 |
Paper |
0.25 |
0.03 |
Elliot & Maier, 2013 - Exp 1 |
Elliot, A. J., & Maier, M. a. (2013). The red-attractiveness effect, applying the Ioannidis and Trikalinos (2007b) test, and the broader scientific context: a reply to Francis (2013). Journal of Experimental Psychology. General, 142(1), 297-300. http://doi.org/10.1037/a0029592 |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
19.47 |
19.47 |
LCh(42.6, 45.2, 15.8) |
LCh(43.0, -, 296.7) |
No |
Yes |
Yes |
75 |
6.29 |
1.35 |
69 |
5.93 |
1.49 |
NA |
NA |
0.62 |
NA |
144 |
NA |
| Elliot & Niesta, 2008 |
Paper |
0.62 |
0.14 |
Elliot & Niesta, 2008 - Exp 4 |
Elliot, A. J., & Niesta, D. (2008). Romantic red: red enhances men's attraction to women. Journal of Personality and Social Psychology, 95(5), 1150-1164. http://doi.org/10.1037/0022-3514.95.5.1150 |
2008.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Green |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.97 |
19.97 |
LCh(46.1, 51.2, 29.3) |
LCh(46.1, 51.0, 147.6) |
Yes |
Yes |
Yes |
16 |
6.29 |
0.89 |
15 |
5.66 |
1.09 |
NA |
NA |
0.58 |
NA |
31 |
NA |
| Elliot & Niesta, 2008 |
Paper |
0.67 |
0.11 |
Elliot & Niesta, 2008 - Exp 3 |
Elliot, A. J., & Niesta, D. (2008). Romantic red: red enhances men's attraction to women. Journal of Personality and Social Psychology, 95(5), 1150-1164. http://doi.org/10.1037/0022-3514.95.5.1150 |
2008.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
20.00 |
20.00 |
LCh(50.0, 58.7, 30.3) |
LCh(50.0, -, 52.6) |
Yes |
Yes |
Yes |
20 |
6.65 |
1.10 |
17 |
5.91 |
1.07 |
NA |
NA |
0.61 |
NA |
37 |
NA |
| Elliot & Niesta, 2008 |
Paper |
0.84 |
0.19 |
Elliot & Niesta, 2008 - Exp 5 |
Elliot, A. J., & Niesta, D. (2008). Romantic red: red enhances men's attraction to women. Journal of Personality and Social Psychology, 95(5), 1150-1164. http://doi.org/10.1037/0022-3514.95.5.1150 |
2008.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.77 |
19.77 |
LCh(45.9, 54.8, 32.5) |
LCh(46.0, 54.9, 283.0) |
Yes |
Yes |
Yes |
12 |
7.21 |
1.05 |
11 |
6.09 |
1.49 |
NA |
NA |
0.64 |
NA |
23 |
NA |
| Elliot & Niesta, 2008 |
Paper |
0.75 |
0.13 |
Elliot & Niesta, 2008 - Exp 2 |
Elliot, A. J., & Niesta, D. (2008). Romantic red: red enhances men's attraction to women. Journal of Personality and Social Psychology, 95(5), 1150-1164. http://doi.org/10.1037/0022-3514.95.5.1150 |
2008.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.27 |
19.27 |
LCh(55.5, 78.0, 28.0) |
No Data |
Yes |
No |
Yes |
16 |
7.07 |
0.78 |
16 |
6.13 |
1.53 |
NA |
NA |
0.64 |
Age includes both male and female participants. |
32 |
NA |
| Elliot & Niesta, 2008 |
Paper |
1.08 |
0.17 |
Elliot & Niesta, 2008 - Exp 1 |
Elliot, A. J., & Niesta, D. (2008). Romantic red: red enhances men's attraction to women. Journal of Personality and Social Psychology, 95(5), 1150-1164. http://doi.org/10.1037/0022-3514.95.5.1150 |
2008.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
20.52 |
20.52 |
LCh(50.3, 58.8, 29.9) |
No Data |
Yes |
No |
Yes |
15 |
7.33 |
0.90 |
12 |
6.25 |
1.05 |
NA |
NA |
0.66 |
NA |
27 |
NA |
| Elliot et al., 2010 |
Paper |
0.82 |
0.13 |
Elliot et al., 2010 - Exp 3 |
Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Red, rank, and romance in women viewing men. Journal of Experimental Psychology: General, 139(3), 399-417. http://doi.org/10.1037/a0019689 |
2010.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
19.64 |
19.64 |
LCh(50.0, 59.6, 31.3) |
LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
16 |
6.69 |
1.22 |
17 |
5.27 |
2.04 |
NA |
NA |
0.53 |
df doesn't match sample size |
33 |
NA |
| Elliot et al., 2010 |
Paper |
0.61 |
0.08 |
Elliot et al., 2010 - Exp 4 |
Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Red, rank, and romance in women viewing men. Journal of Experimental Psychology: General, 139(3), 399-417. http://doi.org/10.1037/a0019689 |
2010.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Green |
Clothing |
Bust |
Same between conditions |
Mehrabian & Blum's Perceived attractiveness |
4 |
1-9 |
1 |
9 |
China |
Asia |
Students |
Undergrads |
Between Subjects |
Chinese |
Chinese |
Chinese |
Matched |
20.60 |
20.60 |
LCh(51.3, 51.7, 30.1) |
LCh(51.5, 51.6, 136.6) |
Yes |
Yes |
Yes |
27 |
6.32 |
1.09 |
28 |
5.50 |
1.50 |
NA |
NA |
0.56 |
NA |
55 |
NA |
| Elliot et al., 2010 |
Paper |
0.90 |
0.21 |
Elliot et al., 2010 - Exp 1 |
Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Red, rank, and romance in women viewing men. Journal of Experimental Psychology: General, 139(3), 399-417. http://doi.org/10.1037/a0019689 |
2010.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
20.19 |
20.19 |
LCh(49.6, 58.8, 30.4) |
No Data |
Yes |
No |
Yes |
10 |
6.79 |
1.00 |
11 |
5.67 |
1.34 |
NA |
NA |
0.58 |
df doesn't match sample size |
21 |
NA |
| Elliot et al., 2010 |
Paper |
0.82 |
0.16 |
Elliot et al., 2010 - Exp 7 |
Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Red, rank, and romance in women viewing men. Journal of Experimental Psychology: General, 139(3), 399-417. http://doi.org/10.1037/a0019689 |
2010.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Clothing |
Bust |
Same between conditions |
Maner et al perceived attractiveness |
1 |
1-9 |
1 |
9 |
England |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.44 |
19.44 |
LCh(54.8, 43.2, 30.3) |
LCh(55.1, 43.7, 283.0) |
Yes |
Yes |
Yes |
12 |
7.50 |
1.17 |
15 |
6.13 |
1.89 |
NA |
NA |
0.64 |
NA |
27 |
NA |
| Elliot et al., 2010 |
Paper |
1.05 |
0.15 |
Elliot et al., 2010 - Exp 2 |
Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Red, rank, and romance in women viewing men. Journal of Experimental Psychology: General, 139(3), 399-417. http://doi.org/10.1037/a0019689 |
2010.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
20.46 |
20.46 |
LCh(49.6, 58.8, 30.4) |
No Data |
Yes |
No |
Yes |
20 |
7.15 |
0.74 |
12 |
6.20 |
1.08 |
NA |
NA |
0.65 |
Sample size taken from Francis, t(df) seems to be using ANOVA df for post-hoc, age data for both male and female participants (separate was not provided) |
32 |
NA |
| Elliot et al., 2013 |
Paper |
0.64 |
0.10 |
Elliot et al., 2013 - Exp 1 |
Elliot, A. J., Tracy, J. L., Pazda, A. D., & Beall, A. T. (2013). Red enhances women's attractiveness to men: First evidence suggesting universality. Journal of Experimental Social Psychology, 49(1), 165-168. http://doi.org/10.1016/j.jesp.2012.07.017 |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Background |
Head Shot |
Same between conditions |
Perceived attractiveness |
3 |
1-5 |
1 |
5 |
Burkina Faso |
Africa |
Adults |
NA |
Between Subjects |
Black |
Black |
Black |
Matched |
26.80 |
26.80 |
LCh(42.7, 51.5, 20.4) |
LCh(43.4, 51.5, 269.8) |
No |
Yes |
Yes |
21 |
4.62 |
0.59 |
21 |
4.14 |
0.85 |
NA |
NA |
0.78 |
NA |
42 |
NA |
| Frazier, 2014 |
Paper |
0.09 |
0.06 |
Frazier, 2014 - Exp 1 |
Frazier, A. (2014, November 13). Fork of Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Retrieved from osf.io/u0mig |
2014.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
18.90 |
18.90 |
LCh(50.0, 59.6, 31.3) |
LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
29 |
6.09 |
1.39 |
39 |
5.97 |
1.26 |
NA |
NA |
0.62 |
NA |
68 |
NA |
| Gilston & Privitera, 2016 |
Screen |
1.92 |
0.04 |
Gilston & Privitera, 2016 - Exp 1 - Healthy |
Gilston, A., & Privitera, G. J. (2015). A 'Healthy' Color: Information About Healthy Eating Attenuates the 'Red Effect.' Global Journal of Health Science, 8(1), 56-61. https://doi.org/10.5539/gjhs.v8n1p56 |
2016.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Head Shot |
Same between conditions |
Perceived attractiveness |
1 |
1-7 |
1 |
7 |
USA |
North America |
Students |
Undergrad |
Within Subjects |
NA |
NA |
White |
NA |
19.85 |
19.85 |
No Data |
No Data |
No |
No |
Yes |
54 |
5.65 |
1.51 |
54 |
3.09 |
1.09 |
NA |
0.89 |
0.35 |
NA |
54 |
1.32 |
| Gueguen, 2012 |
Paper |
0.74 |
0.05 |
Gueguen, 2012 - Exp 1 |
Gueguen, N. (2012). Color and Women Attractiveness: When Red Clothed Women Are Perceived to Have More Intense Sexual Intent. The Journal of Social Psychology, 152(3), 261-265. http://doi.org/10.1080/00224545.2011.605398 |
2012.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue/Green/White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
1 |
1-9 |
1 |
9 |
France |
Europe |
Students |
Undergrads |
Between Subjects |
NA |
NA |
NA |
NA |
19.20 |
19.20 |
No Data |
No Data |
No |
No |
Yes |
30 |
5.95 |
1.24 |
90 |
5.04 |
1.22 |
NA |
NA |
0.50 |
Control is average of blue, white, and green |
120 |
NA |
| Hesslinger et al. 2015 |
Paper |
0.46 |
0.13 |
Hesslinger et al. 2015 - Exp 2 |
Hesslinger, V. M., Goldbach, L., Carbon, C.-C., Allgemeine, A., Psychologie, E., & Note, A. (2015). Men in red: A reexamination of the red-attractiveness effect. Psychonomic Bulletin & Review, 55(4), 1-6. http://doi.org/10.3758/s13423-015-0866-8 |
2015.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Full Body |
Same between conditions |
Perceived attractiveness, German translation |
3 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
20.20 |
20.20 |
CIE-Lab(50, 51, 30) |
No Data |
Yes |
No |
Yes |
16 |
4.98 |
0.70 |
16 |
4.63 |
0.79 |
NA |
NA |
0.45 |
Age includes both male and female participants. |
32 |
NA |
| Hesslinger et al. 2015 |
Paper |
0.06 |
0.06 |
Hesslinger et al. 2015 - Exp 1 |
Hesslinger, V. M., Goldbach, L., Carbon, C.-C., Allgemeine, A., Psychologie, E., & Note, A. (2015). Men in red: A reexamination of the red-attractiveness effect. Psychonomic Bulletin & Review, 55(4), 1-6. http://doi.org/10.3758/s13423-015-0866-8 |
2015.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness, German translation |
3 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
21.20 |
22.60 |
CIE-Lab(50, 51, 30) |
No Data |
Yes |
No |
Yes |
35 |
5.71 |
1.65 |
37 |
5.62 |
1.44 |
NA |
NA |
0.58 |
Age includes both male and female participants. |
72 |
NA |
| Johnson et al., 2015 |
Paper |
-0.01 |
0.05 |
Johnson et al., 2015 - Exp 1 |
Johnson, K., Meltzer, A., & Grahe, J. E. (2015, October 12). Fork of Elliot, A. J., Niesta Kayser, D., Greitemeyer, T., Lichtenfeld, S., Gramzow, R. H., Maier, M. A., & Liu, H. (2010). Retrieved from osf.io/ictud |
2014.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
18.94 |
18.92 |
LCh(50.0, 59.6, 31.3) |
LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
35 |
5.97 |
1.60 |
38 |
5.99 |
1.34 |
NA |
NA |
0.62 |
Yellow group also run, but not included |
73 |
NA |
| Khislavsky, 2016 |
Paper |
0.06 |
0.02 |
Khislavsky, 2016 - Exp 1 |
Khislavsky, A. (2016, March 14). Replication of Elliot et al. (2010). Red, rank, and romance in women viewing men. Retrieved from osf.io/f2udj |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
Latino |
Latino |
Latino |
Matched |
19.91 |
20.04 |
~LCh(50.0, 59.6, 31.3) |
~LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
95 |
5.73 |
1.76 |
92 |
5.61 |
1.84 |
NA |
NA |
0.58 |
Not reviewed by CREP |
187 |
NA |
| Kirsch, 2015 |
Screen |
-0.47 |
0.03 |
Kirsch, 2015 - Exp 1 - Heterosexual |
Kirsch, F. (2015). Wahrgenommene Attraktivitaet und sexuelle Orientierung: Die Wirkung von Rot und Farbpraeferenzen (Perceived attractiveness and sexual orientation: The effects of red and color preferences). Wiesbaden: Springer. doi: 10.1007/978-3-658-08405-9 |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
Germany |
Europe |
Online |
NA |
Between Subjects |
NA |
NA |
White |
NA |
22.45 |
22.45 |
No Data |
No Data |
No |
No |
No |
76 |
5.33 |
1.83 |
85 |
6.13 |
1.54 |
NA |
NA |
0.64 |
Cross-gender rating (females rating males). Age includes participants in all conditions. |
161 |
NA |
| Kirsch, 2015 |
Screen |
0.32 |
0.04 |
Kirsch, 2015 - Exp 1 - Heterosexual |
Kirsch, F. (2015). Wahrgenommene Attraktivitaet und sexuelle Orientierung: Die Wirkung von Rot und Farbpraeferenzen (Perceived attractiveness and sexual orientation: The effects of red and color preferences). Wiesbaden: Springer. doi: 10.1007/978-3-658-08405-9 |
2015.0 |
No |
Monograph |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
Germany |
Europe |
Online |
NA |
Between Subjects |
NA |
NA |
White |
NA |
22.45 |
22.45 |
No Data |
No Data |
No |
No |
No |
57 |
6.85 |
1.44 |
48 |
6.42 |
1.22 |
NA |
NA |
0.68 |
Cross-gender rating (males rating females). Age includes participants in all conditions. |
105 |
NA |
| Kirsch, 2015 |
NA |
0.03 |
0.07 |
Kirsch, 2015 - Exp 2 |
Kirsch, F. (2015). Wahrgenommene Attraktivitaet und sexuelle Orientierung: Die Wirkung von Rot und Farbpraeferenzen (Perceived attractiveness and sexual orientation: The effects of red and color preferences). Wiesbaden: Springer. doi: 10.1007/978-3-658-08405-9 |
2015.0 |
No |
Monograph |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
NA |
NA |
NA |
NA |
NA |
NA |
No Data |
No Data |
No |
No |
No |
28 |
6.55 |
1.17 |
28 |
6.52 |
1.36 |
NA |
NA |
0.69 |
Means are only for cross-gender rating (males rating females) |
56 |
NA |
| Legate et al., 2015 |
Paper |
-0.35 |
0.08 |
Legate et al., 2015 - Exp 1 |
Legate, N., Baciu, C., Horne, L. M., Fiol, S., Paniagua, D., Muqeet, M., & Zachocki, E. (2015, June 27). Replication of Elliot et al. (2010) at IIT. Retrieved from osf.io/zih7c |
2015.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White (21 white, 16 asian) |
Latino |
Mis-match |
20.73 |
20.25 |
~LCh(50.0, 59.6, 31.3) |
~LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
25 |
5.76 |
1.61 |
23 |
6.33 |
1.58 |
NA |
NA |
0.67 |
NA |
48 |
NA |
| Lehmann & Calin |
Screen |
0.39 |
0.07 |
Lehmann & Calin-Jageman, 2015 - Class Exp |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
31.70 |
36.15 |
No Data |
No Data |
No |
No |
No |
29 |
4.34 |
1.63 |
28 |
3.69 |
1.65 |
NA |
NA |
0.34 |
NA |
57 |
NA |
| Lehmann & Calin |
Paper |
-0.11 |
0.03 |
Lehmann & Calin-Jageman, 2017 - Exp 1 |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2017.0 |
Yes |
Journal |
Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
Latino |
Mixed |
White/Latino |
Matched |
20.41 |
21.22 |
LCh(51.3, 58.2, 29.5) |
No Data |
Yes |
No |
Yes |
56 |
4.67 |
2.05 |
60 |
4.89 |
1.80 |
NA |
NA |
0.49 |
NA |
116 |
NA |
| Lehmann & Calin |
Screen |
-0.08 |
0.02 |
Lehmann & Calin-Jageman, 2017 - Exp 2 |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2017.0 |
Yes |
Journal |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White/Latino |
Matched |
36.05 |
38.32 |
No Data |
No Data |
No |
No |
No |
114 |
5.24 |
1.58 |
130 |
5.38 |
1.85 |
NA |
NA |
0.55 |
NA |
244 |
NA |
| Lehmann & Calin |
Screen |
-0.23 |
0.04 |
Lehmann & Calin-Jageman, 2015 - Class Exp |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
33.15 |
33.88 |
No Data |
No Data |
No |
No |
No |
56 |
5.24 |
1.59 |
46 |
5.59 |
1.34 |
NA |
NA |
0.57 |
NA |
102 |
NA |
| Lehmann & Calin |
Screen |
0.10 |
0.02 |
Lehmann & Calin-Jageman, 2017 - Exp 2 |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2017.0 |
Yes |
Journal |
Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
35.78 |
35.85 |
No Data |
No Data |
No |
No |
No |
104 |
6.51 |
1.32 |
106 |
6.38 |
1.32 |
NA |
NA |
0.67 |
NA |
210 |
NA |
| Lehmann & Calin |
Paper |
0.00 |
0.14 |
Lehmann & Calin-Jageman, 2017 - Exp 1 |
Lehmann & Calin-Jageman (2017) Is red really romantic? Direct replications suggest little to no effect of the color red on perceived attractiveness for men and women. Social Psychology. |
2017.0 |
Yes |
Journal |
Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
Mixed |
Mixed |
White |
Mis-match |
20.81 |
20.45 |
LCh(51.3, 58.2, 29.5) |
No Data |
Yes |
No |
Yes |
21 |
6.52 |
1.16 |
11 |
6.52 |
1.56 |
NA |
NA |
0.69 |
NA |
32 |
NA |
| Lin, 2014 |
Paper |
1.53 |
0.13 |
Lin, 2014 - Exp 1 |
Lin, H. (2014). Red-colored products enhance the attractiveness of women. Displays, 35(4), 202-205. http://doi.org/10.1016/j.displa.2014.05.009 |
2014.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Item |
Bust |
Same between conditions |
Single item perceived attractiveness |
1 |
1-5 |
1 |
5 |
Taiwan |
Asia |
Students |
Undergrads |
Between Subjects |
Asian |
NA |
Asian |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
20 |
3.50 |
0.69 |
20 |
2.55 |
0.51 |
NA |
NA |
0.39 |
Control condition is blue; silver condition is dropped as it is not an original control color |
40 |
NA |
| Maves & Nadler, 2016 |
Paper |
-0.12 |
0.03 |
Maves & Nadler, 2016 - Exp 1 |
Maves, M., & Nadler, J. T. (2016, June 2). Data and Analysis. Retrieved from osf.io/9bm8v |
2015.0 |
No |
CREP |
Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
21.86 |
22.48 |
~LCh(50.0, 59.6, 31.3) |
~LCh(50.0, -, 69.1) |
Yes |
Yes |
Yes |
66 |
6.07 |
1.40 |
64 |
6.23 |
1.38 |
NA |
NA |
0.65 |
NA |
130 |
NA |
| O'Mara & Trujillo, 2015 |
Screen |
0.97 |
0.10 |
O'Mara & Trujillo, 2015 - Exp 1 - Masculine Face |
O'Mara, E. M., & Trujillo, A. (2015), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Head Shot |
Same between conditions |
Perceived attractiveness |
1 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.10 |
19.10 |
NA |
NA |
No |
No |
Yes |
21 |
6.11 |
1.30 |
25 |
4.78 |
1.38 |
NA |
NA |
0.47 |
NA |
46 |
NA |
| O'Mara & Trujillo, 2015 |
Screen |
-0.20 |
0.09 |
O'Mara & Trujillo, 2015 - Exp 2 - Masculine Face |
O'Mara, E. M., & Trujillo, A. (2015), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Background |
Head Shot |
Same between conditions |
Perceived attractiveness |
1 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
28.23 |
28.23 |
NA |
NA |
No |
No |
No |
24 |
4.88 |
1.84 |
21 |
5.23 |
1.61 |
NA |
NA |
0.53 |
NA |
45 |
NA |
| O'Mara et al., 2016 |
Screen |
0.45 |
0.14 |
O'Mara et al., 2016 - Exp 2 - Long Shirt |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.26 |
19.26 |
NA |
NA |
No |
No |
Yes |
20 |
4.42 |
1.37 |
12 |
3.79 |
1.41 |
NA |
NA |
0.35 |
NA |
32 |
NA |
| O'Mara et al., 2016 |
Screen |
-0.32 |
0.14 |
O'Mara et al., 2016 - Exp 2 - Tank Top |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.26 |
19.26 |
NA |
NA |
No |
No |
Yes |
17 |
3.91 |
1.09 |
12 |
4.33 |
1.51 |
NA |
NA |
0.42 |
NA |
29 |
NA |
| O'Mara et al., 2016 |
Screen |
0.47 |
0.07 |
O'Mara et al., 2016 - Exp 1 - Long Shirt |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
34.56 |
34.56 |
NA |
NA |
No |
No |
No |
28 |
6.07 |
2.14 |
35 |
5.12 |
1.89 |
NA |
NA |
0.52 |
NA |
63 |
NA |
| O'Mara et al., 2016 |
Screen |
0.10 |
0.06 |
O'Mara et al., 2016 - Exp 1 - Tank Top |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
34.56 |
34.56 |
NA |
NA |
No |
No |
No |
34 |
5.53 |
1.96 |
35 |
5.33 |
2.11 |
NA |
NA |
0.54 |
NA |
69 |
NA |
| O'Mara et al., 2016 |
Screen |
-0.12 |
0.04 |
O'Mara et al., 2016 - Exp 3 - Tank Top |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2016.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.54 |
19.54 |
NA |
NA |
No |
No |
Yes |
51 |
6.70 |
1.14 |
55 |
6.83 |
1.00 |
NA |
NA |
0.73 |
NA |
106 |
NA |
| O'Mara et al., 2016 |
Screen |
-0.14 |
0.03 |
O'Mara et al., 2016 - Exp 3 - Long Shirt |
O'Mara, E. M., Kershaw, C., Receveur, A., Hunt, C., Askar, S., Ballas, T., Farmer, C., O'Koon, B., Stitzel, C., Vavro, C., & Wilhoit, S. (2016), unpublished data. |
2016.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Different between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.54 |
19.54 |
NA |
NA |
No |
No |
Yes |
63 |
6.97 |
1.27 |
57 |
7.12 |
0.93 |
NA |
NA |
0.77 |
NA |
120 |
NA |
| Pazda et al., 2012 |
Paper |
0.63 |
0.09 |
Pazda et al., 2012 - Exp 2 |
Pazda, A. D., Elliot, A. J., & Greitemeyer, T. (2012). Sexy red: Perceived sexual receptivity mediates the red-attraction relation in men viewing woman. Journal of Experimental Social Psychology, 48(3), 787-790. http://doi.org/10.1016/j.jesp.2011.12.009 |
2012.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Green |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
Austria |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
23.50 |
23.50 |
LCh(40.6, 40.4, 20.1) |
LCh(40.3, 41.2, 146.8) |
No |
Yes |
Yes |
27 |
6.07 |
1.17 |
22 |
5.00 |
2.13 |
NA |
NA |
0.50 |
NA |
49 |
NA |
| Pazda et al., 2014 |
Screen |
0.32 |
0.02 |
Pazda et al., 2014 - Exp 1 |
Pazda, A. D., Elliot, A. J., & Greitemeyer, T. (2014). Perceived sexual receptivity and fashionableness: Separate paths linking red and black to perceived attractiveness. Color Research & Application, 39(2), 208-212. http://doi.org/10.1002/col.21804 |
2014.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Full Body |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
Not specified |
Unknown |
Online |
Mturk |
Between Subjects |
White |
White (170 white, 142 Asian) |
White |
Matched |
24.50 |
24.50 |
No Data |
No Data |
No |
No |
No |
109 |
6.03 |
1.78 |
125 |
5.46 |
1.77 |
NA |
NA |
0.56 |
NA |
234 |
NA |
| Pazda et al., 2017 |
Screen |
0.17 |
0.00 |
Pazda et al., 2017 - Exp 1 |
Pazda, A., Thorstenson & Elliot, A. (2017). Unpublished data. |
2017.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Green |
Clothing |
Full Body |
Same between conditions |
Single Item |
1 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Lab study |
Within Subjects |
NA |
NA |
White |
NA |
19.76 |
NA |
red LCh(42.00, 57.92, 348.89), green LCh(41.50, 56.71, 92.17) |
NA |
No |
Yes |
Yes |
115 |
7.81 |
1.21 |
115 |
7.58 |
1.41 |
NA |
0.84 |
0.82 |
NA |
115 |
1.31 |
| Pazda et al., 2017 |
Screen |
0.10 |
0.00 |
Pazda et al., 2017 - Exp 2 |
Pazda, A., Thorstenson & Elliot, A. (2017). Unpublished data. |
2017.0 |
No |
Unpublished/Online |
Pre-Registered |
No |
Romantic |
Males |
Green |
Clothing |
Full Body |
Same between conditions |
Single Item |
1 |
1-9 |
1 |
9 |
USA |
North America |
Online |
Mturk |
Within Subjects |
White |
NA |
White |
Matched |
37.43 |
NA |
red LCh(42.00, 57.92, 348.89), green LCh(41.50, 56.71, 92.17) |
NA |
No |
No |
No |
228 |
8.08 |
1.28 |
228 |
7.95 |
1.39 |
NA |
0.80 |
0.87 |
NA |
228 |
1.34 |
| Peperkoorn et al., 2016 |
Paper |
-0.43 |
0.06 |
Peperkoorn et al., 2016 - Exp 1 - Short Term |
Peperkoorn, L. S., Roberts, S. C., & Pollet, T. V. (2016). Revisiting the Red Effect on Attractiveness and Sexual Receptivity: No Effect of the Color Red on Human Mate Preferences. Evolutionary Psychology, 14(4). http://doi.org/10.1177/1474704916673841 |
2016.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-11 |
2 |
22 |
Netherlands |
Europe |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
23.67 |
23.67 |
NA |
NA |
No |
No |
Yes |
34 |
14.26 |
3.31 |
34 |
15.47 |
2.18 |
NA |
NA |
0.67 |
NA |
68 |
NA |
| Peperkoorn et al., 2016 |
Screen |
-0.10 |
0.06 |
Peperkoorn et al., 2016 - Exp 2 - Short Term |
Peperkoorn, L. S., Roberts, S. C., & Pollet, T. V. (2016). Revisiting the Red Effect on Attractiveness and Sexual Receptivity: No Effect of the Color Red on Human Mate Preferences. Evolutionary Psychology, 14(4). http://doi.org/10.1177/1474704916673841 |
2016.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-11 |
2 |
22 |
USA |
North America |
Online |
Mturk |
Between Subjects |
White |
White |
White |
Matched |
30.13 |
30.13 |
NA |
NA |
No |
No |
No |
33 |
15.06 |
4.14 |
36 |
15.47 |
3.61 |
NA |
NA |
0.67 |
NA |
69 |
NA |
| Pollet, 2013 |
Screen |
0.16 |
0.08 |
Pollet, 2013 - Exp 1 |
Pollet T. (2013). Unpublished data |
2013.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Clothing |
Full Body |
Same between conditions |
Single item |
1 |
1-7 |
1 |
7 |
Netherlands |
Europe |
Students |
NA |
Between Subjects |
White |
Primarily dutch nationality |
White |
Matched |
26.60 |
28.40 |
No Data |
No Data |
No |
No |
No |
26 |
3.15 |
1.22 |
23 |
2.96 |
1.19 |
NA |
NA |
0.33 |
Only blue control color used as other control colors were not in original |
49 |
NA |
| Purdy, 2009 |
Screen |
0.30 |
0.16 |
Purdy, 2009 - Exp 1 - High Arousal |
Purdy, M. A. (2009). The influence of the amygdala and color on judgments of attractiveness. UNC Asheville Journal, Undergraduate Research Program, Asheville, NC |
2009.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
NA |
NA |
White |
NA |
21.00 |
21.00 |
RGB(185, 26, 23) |
RGB(216,216,216) |
No |
No |
Yes |
13 |
7.26 |
3.27 |
13 |
6.24 |
3.27 |
NA |
NA |
0.66 |
NA |
26 |
NA |
| Purdy, 2009 |
Screen |
0.01 |
0.15 |
Purdy, 2009 - Exp 1 - Low Arousal |
Purdy, M. A. (2009). The influence of the amygdala and color on judgments of attractiveness. UNC Asheville Journal, Undergraduate Research Program, Asheville, NC |
2009.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
NA |
NA |
White |
NA |
21.00 |
21.00 |
RGB(185, 26, 23) |
RGB(216,216,216) |
No |
No |
Yes |
13 |
6.37 |
3.31 |
13 |
6.33 |
3.27 |
NA |
NA |
0.67 |
NA |
26 |
NA |
| Roberts et al., 2010 |
Screen |
0.33 |
0.05 |
Roberts et al., 2010 - Exp 2 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue/Green/White |
Clothing |
Bust |
Different between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
15 |
3.66 |
0.60 |
15 |
3.45 |
0.61 |
NA |
0.66 |
0.27 |
Age range includes both male and female participants. |
15 |
0.60 |
| Roberts et al., 2010 |
Screen |
0.40 |
0.02 |
Roberts et al., 2010 - Exp 2 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue/Green/White |
Clothing |
Bust |
Different between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
15 |
3.65 |
0.45 |
15 |
3.46 |
0.48 |
NA |
0.92 |
0.27 |
Age range includes both male and female participants. |
15 |
0.47 |
| Roberts et al., 2010 |
Screen |
0.19 |
0.02 |
Roberts et al., 2010 - Exp 1 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue/Green/White |
Clothing |
Bust |
Different between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
30 |
4.50 |
1.23 |
30 |
4.26 |
1.18 |
NA |
0.66 |
0.36 |
Age range includes both male and female participants. |
30 |
1.21 |
| Roberts et al., 2010 |
Screen |
0.19 |
0.01 |
Roberts et al., 2010 - Exp 1 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue/Green/White |
Clothing |
Bust |
Different between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
30 |
4.60 |
1.10 |
30 |
4.40 |
0.92 |
NA |
0.92 |
0.38 |
Age range includes both male and female participants. |
30 |
1.01 |
| Roberts et al., 2010 |
Screen |
-0.08 |
0.01 |
Roberts et al., 2010 - Exp 3 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Bust |
Same between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
25 |
4.82 |
0.90 |
25 |
4.88 |
0.85 |
0.36 |
0.92 |
0.43 |
Age range includes both male and female participants. |
25 |
0.88 |
| Roberts et al., 2010 |
Screen |
-0.05 |
0.03 |
Roberts et al., 2010 - Exp 3 |
Roberts, S. C., Owen, R. C., & Havlicek, J. (2010). Distinguishing between Perceiver and Wearer Effects in Clothing Color-Associated Attributions. Evolutionary Psychology, 8(3), 350-364. http://doi.org/10.1177/147470491000800304 |
2010.1 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
White |
Clothing |
Bust |
Same between conditions |
Single item rating of attractiveness |
1 |
1-10 |
1 |
10 |
England |
Europe |
Students |
Undergrads |
Within Subjects |
White |
Noted in manuscript all caucasian |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
23 |
4.87 |
0.75 |
23 |
4.90 |
0.73 |
0.61 |
0.66 |
0.43 |
Age range includes both male and female participants. |
23 |
0.74 |
| Schwarz & Singer, 2013 |
Paper |
0.19 |
0.07 |
Schwarz & Singer, 2013 - Exp 1 - Adults Rate Young |
Schwarz, S., & Singer, M. (2013). Romantic red revisited: Red enhances men's attraction to young, but not menopausal women. Journal of Experimental Social Psychology, 49(1), 161-164. http://doi.org/10.1016/j.jesp.2012.08.004 |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
1 |
1-9 |
1 |
9 |
Germany |
Europe |
Adults |
NA |
Between Subjects |
NA |
NA |
White |
NA |
53.47 |
53.47 |
Lum: 35.2, Chroma: 39.3, Hue no specified |
No Data |
No |
No |
Yes |
30 |
6.53 |
1.96 |
30 |
6.13 |
2.17 |
NA |
NA |
0.64 |
NA |
60 |
NA |
| Schwarz & Singer, 2013 |
Paper |
-0.15 |
0.07 |
Schwarz & Singer, 2013 - Exp 1 - UGrads Rate Young |
Schwarz, S., & Singer, M. (2013). Romantic red revisited: Red enhances men's attraction to young, but not menopausal women. Journal of Experimental Social Psychology, 49(1), 161-164. http://doi.org/10.1016/j.jesp.2012.08.004 |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
1 |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads |
Between Subjects |
NA |
NA |
White |
NA |
24.67 |
24.67 |
Lum: 35.2, Chroma: 39.3, Hue no specified |
No Data |
No |
No |
Yes |
30 |
6.20 |
1.42 |
30 |
6.40 |
1.18 |
NA |
NA |
0.68 |
NA |
60 |
NA |
| Seibt & Klement, 2015 |
Screen |
0.22 |
0.05 |
Seibt & Klement, 2015 - Exp 1 |
Seibt, T., & Klement, V. (2015). The Impact of the Colour Red on Attractiveness Perception. In 4th Advanced Research in Scientific Areas (pp. 20-24). http://doi.org/10.18638/arsa.2015.4.1.799 |
2015.0 |
No |
Conference Proceedings |
Not Pre-Registered |
No |
Romantic |
Females |
Green |
Background |
NA |
Same between conditions |
Perceived Attractiveness, subscale of Haselton und Gangestad (2006) |
NA |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads and Grads |
Between Subjects |
NA |
NA |
NA |
NA |
26.70 |
26.70 |
RGB(255.0.0) |
RGB(0.139.0) |
No |
No |
No |
54 |
3.19 |
0.53 |
31 |
3.07 |
0.55 |
NA |
NA |
0.26 |
NA |
85 |
NA |
| Seibt & Klement, 2015 |
Screen |
0.20 |
0.16 |
Seibt & Klement, 2015 - Exp 1 |
Seibt, T., & Klement, V. (2015). The Impact of the Colour Red on Attractiveness Perception. In 4th Advanced Research in Scientific Areas (pp. 20-24). http://doi.org/10.18638/arsa.2015.4.1.799 |
2015.0 |
No |
Conference Proceedings |
Not Pre-Registered |
No |
Romantic |
Males |
Green |
Background |
NA |
Same between conditions |
Perceived Attractiveness, subscale of Haselton und Gangestad (2006) |
NA |
1-9 |
1 |
9 |
Germany |
Europe |
Students |
Undergrads and Grads |
Between Subjects |
NA |
NA |
NA |
NA |
26.70 |
26.70 |
RGB(255.0.0) |
RGB(0.139.0) |
No |
No |
No |
12 |
3.40 |
0.43 |
14 |
3.30 |
0.54 |
NA |
NA |
0.29 |
NA |
26 |
NA |
| Seibt, 2015 |
Screen |
0.20 |
0.05 |
Seibt, 2015 - Exp 1 |
Seibt, T. (2015). Romantic Red Effect in the Attractiveness Perception. In Hassacc (pp. 31-34). http://doi.org/10.18638/hassacc.2015.3.1.186 |
2015.0 |
No |
Conference Proceedings |
Not Pre-Registered |
No |
Romantic |
Males |
Green |
Background |
NA |
Same between conditions |
Perceived Attractiveness |
NA |
1-5 |
1 |
5 |
Germany |
Europe |
Students |
Undergrads and Grads |
Between Subjects |
NA |
NA |
NA |
NA |
25.50 |
25.50 |
No Data |
No Data |
No |
No |
No |
46 |
2.80 |
0.49 |
41 |
2.70 |
0.52 |
NA |
NA |
0.42 |
NA |
87 |
NA |
| Stefan & Gueguen, 2013 |
Paper |
0.62 |
0.12 |
Stefan & Gueguen, 2013 - Exp 1 |
Stefan J. & Gueguen, N. (2013). Unpublished data. |
2013.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
White |
Clothing |
Full Body |
Same between conditions |
Single item |
1 |
1-100 |
1 |
100 |
France |
Europe |
Students |
Undergrads and Grads |
Between Subjects |
White |
White |
White |
Matched |
22.11 |
22.11 |
NA |
NA |
No |
No |
Yes |
18 |
81.33 |
16.30 |
16 |
67.50 |
26.87 |
NA |
NA |
0.67 |
Data provided by Elliot |
34 |
NA |
| Sullivan et al., 2016 |
Screen |
0.24 |
0.04 |
Sullivan et al., 2016 - Exp 1 |
Sullivan, J., Amaral Lavoie, E., Bays, R. B., Fontana, S., Goodkind, R., Johnson, R., ... Lavoie, M. (2016, April 4). Replication of Elliot et al., 2010: Red, Rank, and Romance. Retrieved from osf.io/pm7fx |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
19.96 |
19.45 |
No Data |
No Data |
No |
No |
Yes |
49 |
5.60 |
1.37 |
53 |
5.26 |
1.42 |
NA |
NA |
0.53 |
Two-year class project posted on OSF |
102 |
NA |
| Sullivan et al., 2016 |
Screen |
-0.34 |
0.06 |
Sullivan et al., 2016 - Exp 2 |
Sullivan, J., Amaral Lavoie, E., Bays, R. B., Fontana, S., Goodkind, R., Johnson, R., ... Lavoie, M. (2016, April 4). Replication of Elliot et al., 2010: Red, Rank, and Romance. Retrieved from osf.io/pm7fx |
2016.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Females |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
Latino |
Mis-match |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
38 |
4.85 |
1.65 |
27 |
5.37 |
1.38 |
NA |
NA |
0.55 |
Age recorded as dichotomy (younger then 20, older than 20) so not included |
65 |
NA |
| Sullivan et al., 2016 |
Screen |
0.42 |
0.04 |
Sullivan et al., 2016 - Exp 1 |
Sullivan, J., Amaral Lavoie, E., Bays, R. B., Fontana, S., Goodkind, R., Johnson, R., ... Lavoie, M. (2016, April 4). Replication of Elliot et al., 2010: Red, Rank, and Romance. Retrieved from osf.io/pm7fx |
2015.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
19.62 |
19.75 |
No Data |
No Data |
No |
No |
Yes |
45 |
6.21 |
1.38 |
48 |
5.58 |
1.56 |
NA |
NA |
0.57 |
NA |
93 |
NA |
| Sullivan et al., 2016 |
Screen |
0.02 |
0.12 |
Sullivan et al., 2016 - Exp 2 |
Sullivan, J., Amaral Lavoie, E., Bays, R. B., Fontana, S., Goodkind, R., Johnson, R., ... Lavoie, M. (2016, April 4). Replication of Elliot et al., 2010: Red, Rank, and Romance. Retrieved from osf.io/pm7fx |
2016.0 |
No |
Unpublished/Online |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
3 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White |
White |
Matched |
NA |
NA |
No Data |
No Data |
No |
No |
Yes |
21 |
6.24 |
1.29 |
14 |
6.21 |
1.45 |
NA |
NA |
0.65 |
Age recorded as dichotomy (younger then 20, older than 20) so not included |
35 |
NA |
| Wartenberg et al., 2011 |
Screen |
0.20 |
0.01 |
Wartenberg et al., 2011 - Exp 1 - In Group |
Wartenberg, W., Hoepfner, T., Potthast, P., & Mirau, A. (2011). If you wear red on a date, you will please your mate. Proceedings of Empiriepraktikumskongress, 6th, Aug. 7, pp 26-27. University of Jena, Germany. |
2011.0 |
No |
Conference Proceedings |
Not Pre-Registered |
No |
Romantic |
Females |
Blue |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
4 |
1-7 |
1 |
7 |
Germany |
Europe |
Students |
Undergrads |
Within Subjects |
White |
White |
White |
Matched |
21.47 |
21.47 |
No Data |
No Data |
No |
No |
Yes |
39 |
3.00 |
1.18 |
39 |
2.76 |
1.13 |
0.63 |
0.86 |
0.29 |
Translation of summary provided by Elliot; within subjects info still needed |
39 |
1.16 |
| Wen et al., 2014 |
Paper |
0.16 |
0.07 |
Wen et al., 2014 - Exp 1 - Feminine Females |
Wen, F., Zuo, B., Wu, Y., Sun, S., & Liu, K. (2014). Red is Romantic, but Only for Feminine Females: Sexual Dimorphism Moderates Red Effect on Sexual Attraction. Evolutionary Psychology, 12(4), 719-735. http://doi.org/10.1177/147470491401200404 |
2014.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue/White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness, extracted factor |
3 |
1-7 |
1 |
7 |
China |
Asia |
Students |
Undergrads |
Between Subjects |
Asian |
Asian |
Asian |
Matched |
20.95 |
20.95 |
LCh(51.1, 57.7, 27.8) |
LCh(51.6, 57.6, 278.3) |
Yes |
Yes |
Yes |
22 |
0.24 |
0.93 |
44 |
0.10 |
0.81 |
NA |
NA |
NA |
Control is average of blue and white conditions; only normalized scores provided. Age range includes participants in all conditions. |
66 |
NA |
| Wen et al., 2014 |
Paper |
-0.08 |
0.07 |
Wen et al., 2014 - Exp 1 - Masculine Males |
Wen, F., Zuo, B., Wu, Y., Sun, S., & Liu, K. (2014). Red is Romantic, but Only for Feminine Females: Sexual Dimorphism Moderates Red Effect on Sexual Attraction. Evolutionary Psychology, 12(4), 719-735. http://doi.org/10.1177/147470491401200404 |
2014.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Females |
Blue/White |
Clothing |
Bust |
Same between conditions |
Perceived attractiveness, extracted factor |
3 |
1-7 |
1 |
7 |
China |
Asia |
Students |
Undergrads |
Between Subjects |
Asian |
Asian |
Asian |
Matched |
20.95 |
20.95 |
LCh(51.1, 57.7, 27.8) |
LCh(51.6, 57.6, 278.3) |
Yes |
Yes |
Yes |
21 |
-0.10 |
0.93 |
49 |
-0.03 |
0.85 |
NA |
NA |
NA |
Control is average of blue and white conditions; only normalized scores provided. Age range includes participants in all conditions. |
70 |
NA |
| Williams & Neelon, 2013 |
Screen |
0.58 |
0.13 |
Williams & Neelon, 2013 - Exp 1 - All |
Williams, C. L. & Neelon, M. (2013). Conditional beauty: The impact of emotionally linked images on the red effect in sexual attraction. Psi Chi Journal of Psychological Research, 18(1), 10-19. |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White (noted by authors) |
White |
Matched |
22.50 |
22.50 |
RGB(183,70,60) |
RGB(76,105,200) |
No |
No |
Yes |
16 |
6.81 |
1.03 |
15 |
6.15 |
1.20 |
NA |
NA |
0.64 |
Data provided by Elliot |
31 |
NA |
| Williams & Neelon, 2013 |
Screen |
-0.13 |
0.08 |
Williams & Neelon, 2013 - Exp 2 - Positive and Neutral |
Williams, C. L. & Neelon, M. (2013). Conditional beauty: The impact of emotionally linked images on the red effect in sexual attraction. Psi Chi Journal of Psychological Research, 18(1), 10-19. |
2013.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue |
Background |
Bust |
Same between conditions |
Perceived attractiveness |
2 |
1-9 |
1 |
9 |
USA |
North America |
Students |
Undergrads |
Between Subjects |
White |
White (noted by authors) |
White |
Matched |
21.50 |
21.50 |
RGB(183,70,60) |
RGB(76,105,200) |
No |
No |
Yes |
26 |
6.40 |
1.28 |
26 |
6.56 |
1.04 |
NA |
NA |
0.69 |
Data provided by Elliot |
52 |
NA |
| Young, 2015 |
Screen |
0.14 |
0.00 |
Young, 2015 - Exp 1 - More Attractive |
Young, S. G. (2015). The effect of red on male perceptions of female attractiveness: Moderation by baseline attractiveness of female faces. European Journal of Social Psychology, 45(2), 146-151. http://doi.org/10.1002/ejsp.2098 |
2015.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Gray |
Background |
Head Shot |
Same between conditions |
Single item |
1 |
1-7 |
1 |
7 |
USA |
North America |
Students |
Undergrads |
Within Subjects |
Mixed |
Mixed |
White |
Mis-match |
19.90 |
19.90 |
LCh(62.7, 84.6, 34.1) |
LCh(62.6, -, 265.5) |
No |
Yes |
Yes |
19 |
4.29 |
0.86 |
19 |
4.17 |
0.81 |
0.23 |
0.96 |
0.53 |
NA |
19 |
0.84 |
| Young, 2015 |
Screen |
0.10 |
0.00 |
Young, 2015 - Exp 2 - More Attractive |
Young, S. G. (2015). The effect of red on male perceptions of female attractiveness: Moderation by baseline attractiveness of female faces. European Journal of Social Psychology, 45(2), 146-151. http://doi.org/10.1002/ejsp.2098 |
2015.0 |
Yes |
Journal |
Not Pre-Registered |
No |
Romantic |
Males |
Blue/Gray |
Background |
Head Shot |
Same between conditions |
Single item |
1 |
1-7 |
1 |
7 |
USA |
North America |
Students |
Undergrads |
Within Subjects |
Mixed |
Mixed |
White |
Mis-match |
21.10 |
21.10 |
LCh(62.7, 84.6, 34.1) |
LCh(62.7, 84.6, 34.1) |
No |
Yes |
Yes |
46 |
4.30 |
1.11 |
46 |
4.19 |
1.07 |
0.25 |
0.98 |
0.53 |
Blue and Gray ratings averaged, then compared to red; original data provided |
46 |
1.09 |